[CERC2017]Intrinsic Interval

发表于 2021-10-09 更新于 2021-10-21

思维好题。
先来看一下区间的性质

第一个性质很显然，那么就来证明一下第二个性质。
假设两个区间的交不是区间，则两个区间的交是有空缺的，那么这个空缺的数显然只能在两个区间中的一个里面，那么另一个区间就不连续了，那么就不是区间了。所以两个区间的交还是区间。

那么第二个性质有什么用呢？我们可以从第二个性质得出一个结论：一个子串的本征区间的右端点一定是所有包含这个子串的区间里最靠左的 所以我们就只需要找到询问子串右侧最近的一个区间右端点（即存在一个左端点和它构成区间的点）即可。证明：

假设询问子串右侧最近的一个区间右端点右侧还有一个区间右端点，且所在区间长度更长，那么显然左端点要更靠右，但是两个区间的交还是区间，所以这个左端点可以是询问子串右侧最近的一个区间右端点对应的左端点。

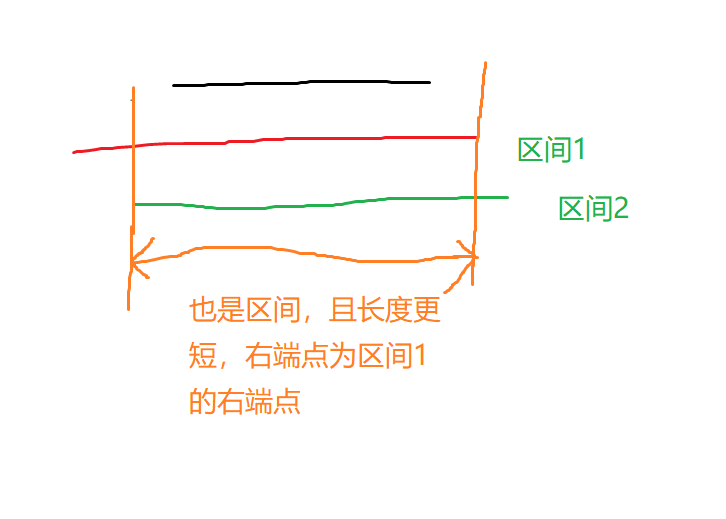
然后问题就是如何判断一个子串是否是区间。
$val[i]$ 表示区间 $[i,i]$ 的值
先另 $val[i] = i$
可以将询问离线下来，按右端点排序，每次移动右端点时用线段树执行下面的操作

1 2	if(a[i]>1&&p[a[i]-1]<=i) upd(1,p[a[i]-1]); if(a[i]<n&&p[a[i]+1]<=i) upd(1,p[a[i]+1]);

$upd(l, r)$ 表示给区间 $[l, r]$ 加 $1$
如果 $val[l] = r$ 则 $[l, r]$ 是好区间
因为每个右端点只会对 $1$ 到左侧相邻数的位置加 $1$ , 所以 $val[l]$ 维护的是 $[l, r]$ 的相邻数对的个数.
code

区间的性质