空间宝石

标签

最短路 + $floyd$ + 线段树

【雅礼2019.10.17amT1】排列

标签

计数 + 二项式反演 + $FFT$ + 图论

$OI$ 之神啊，请赐予我力量

link

标签

线段树

思路

思维好题。
先来看一下区间的性质

1. $Max - Min = r - l$
2. 两个区间的交还是区间
3. 相邻点对的个数等于 $r - l$

第一个性质很显然， 那么就来证明一下第二个性质。
假设两个区间的交不是区间， 则两个区间的交是有空缺的，那么这个空缺的数显然只能在两个区间中的一个里面，那么另一个区间就不连续了，那么就不是区间了。所以两个区间的交还是区间。

那么第二个性质有什么用呢？我们可以从第二个性质得出一个结论 ：一个子串的本征区间的右端点一定是所有包含这个子串的区间里最靠左的 所以我们就只需要找到询问子串右侧最近的一个区间右端点（即存在一个左端点和它构成区间的点）即可。证明：

假设询问子串右侧最近的一个区间右端点右侧还有一个区间右端点，且所在区间长度更长，那么显然左端点要更靠右，但是两个区间的交还是区间，所以这个左端点可以是询问子串右侧最近的一个区间右端点对应的左端点。

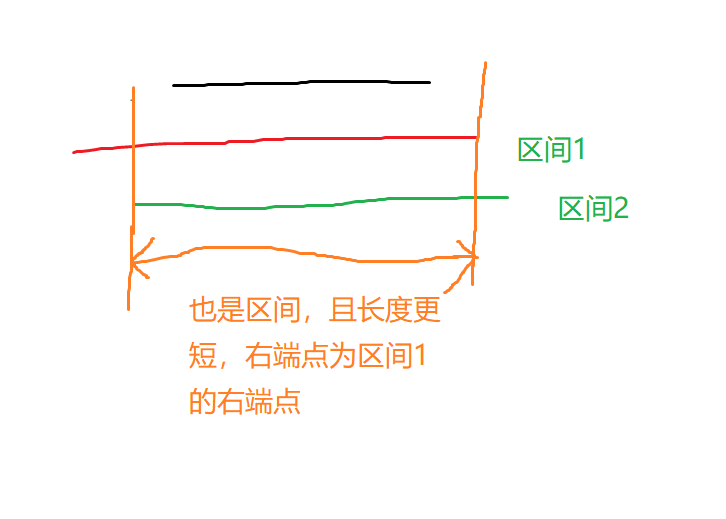
然后问题就是如何判断一个子串是否是区间。
$val[i]$ 表示区间 $[i,i]$ 的值
先另 $val[i] = i$
可以将询问离线下来， 按右端点排序，每次移动右端点时用线段树执行下面的操作

1
2

if(a[i]>1&&p[a[i]-1]<=i) upd(1,p[a[i]-1]);
if(a[i]<n&&p[a[i]+1]<=i) upd(1,p[a[i]+1]);

$upd(l, r)$ 表示给区间 $[l, r]$ 加 $1$
如果 $val[l] = r$ 则 $[l, r]$ 是好区间
因为每个右端点只会对 $1$ 到左侧相邻数的位置加 $1$ , 所以 $val[l]$ 维护的是 $[l, r]$ 的相邻数对的个数.
code

悟

区间的性质

1. $Max - Min = r - l$
2. 两个区间的交还是区间
3. 相邻点对的个数等于 $r - l$

莫比乌斯反演

$[n=1] = \sum_{d|n}\mu(d)$

$G(n) = \sum_{d|n}F(d) \Leftrightarrow F(n) = \sum_{d|n}\mu(\frac{n}{d})G(d)$

标签

期望 + 基环树

标签

暴力 + 分块

标签

数学 + $dp$ + $计数$

第 $k$ 小子序列和

先把所有数从小到大排序.
设一个二元组 $(sum, i)$ , 表示以第 $i$ 位为结尾, 和为 $sum$ 的子序列, 建一个小根堆来维护这些二元组, 每次取出堆顶, 然后把 $(sum + a_{i + 1}, i + 1)$ 和 $(sum + a_{i+1} - a_i, i + 1)$ 加入堆中, 即把第 $i+1$ 个数加入到序列中, 或把序列中最大的数替换成第 $i+1$ 个数. 显然这样可以不重不漏地按顺序遍历完所有情况.

然后第 $k$ 个被取出堆顶的数就是答案.

例题

第 $k$ 大子段和.

设一个三元组 $(o, l, r)$ 表示左端点位置是 $o$, 右端点在 $[l,r]$ 的子段, 定义这个三元组的值为这些子段和的最大值, 即 $\max_{i=l}^{r} (sum_i - sum_{o - 1}) = \max_{i=l}^{r} (sum_i ) - sum_{o - 1}$, 用大根堆来维护, 如果从堆顶取出的是 $(o, l, r)$ , 那么找出最大的 $sum_x$ , 既然已经选了左端点为 $o$, 右端点为 $x$ 的子段, 那么就把三元组一分为二, 分成 $(o, l, x - 1)$ 和 $(o, x + 1, r)$

然后第 $k$ 个被取出堆顶的数就是答案.

例题 题解

总结

这两类问题都灵活的运用了堆, 所以可以总结出求第 $k$ 大的一种方法:
把当前有的情况放到堆中, 每次从堆中取出堆顶, 并拓展出其它情况放入堆中. 这样重复 $k$ 次.
但前提是用这种方法必须要 能够 不重不漏地按顺序遍历完所有情况, 即第 $k$ 次从堆顶取出的值必须是第 $k$ 大值(或第 $k$ 小值).

背包问题

标签

$lis$ + $dp$