CF235D Graph Game

标签

期望 + 基环树

思路

先考虑树的做法, 对于两个点 $u$ 和 $v$, $v$ 在 $u$ 的点分树内等价于 $u$ 成为重心时 $u$ 和 $v$ 连通， 即 $u$ 是 $u$ 到 $v$ 的路径上最早成为重心的点。显然概率为 $\frac{1}{dis(u, v) + 1}$, 那么答案就是 $\sum_{u\in V} \sum_{v \in V} \frac{1}{dis(u, v) + 1}$

接着考虑拓展到基环树上，对于在同一棵树上的点，和树上的做法一样。对于不在同一棵树上的点，就要把环考虑进去，那么路径可以分为三个部分， 分别是两个半环和一条链，如图所示：

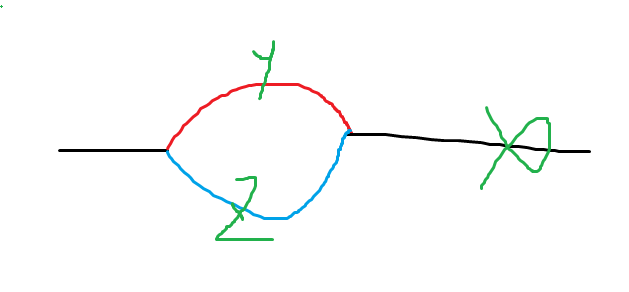
那么$u$ 成为重心时 $u$ 和 $v$ 联通只需要 $u$ 是 $x$ 和 $y$ 中最先成为重心的点或 $u$ 是 $x$ 和 $z$ 中最先成为重心的点，这个概率是 $\frac{1}{x + y + 1}+\frac{1}{x + z + 1}-\frac{1}{x + y + z}$, 即 $u$ 是 $x$ 和 $y$ 中最先成为重心的点的概率加上 $u$ 是 $x$ 和 $z$ 中最先成为重心的点的概率再减去 $u$ 同时是 $x$ , $y$, $z$ 中最先成为重心的点的概率. 本质上是一个容斥。

Code

悟

1. 基环树上的问题可以先考虑树上的做法，然后拓展到基环树上。仙人掌有些题也是这样。
2. $v$ 在 $u$ 的点分树内等价于 $u$ 是 $u$ 到 $v$ 的路径上最早成为重心的点

坑

略